What is the Angle of Depression?
Angle of Depresson Definition
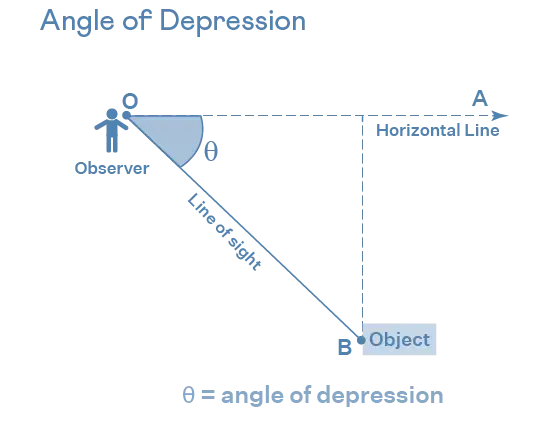
The angle of depression is defined as the angle between the object and the observer looking at the object. It is the angle between the horizontal line and the observer's line of sight. In trigonometry, the horizontal line may refer to the triangle's base, and the line of sight may refer to the perpendicular. In other words, the angle of depression depends on two factors, base and perpendicular.
For example, if a man is looking down to an object far at a horizontal distance. Then, the angle formed between the observer and the object is called the angle of depression. It means that if the angle between the object and the observer is in a downward direction, it is called the angle of depression.
Angle of Depression Formula
The basic knowledge of all trigonometric ratios are required to find any angle and height of a right-angled triangle. These trigonometric ratios are sine, cosine and tangent. Since triangle formed by the angle of depression is right-angled, so the using the trigonometric ratio the angle of depression formula is
$$ θ\;=\;tan^{-1}\;(\frac{vertical\;distance}{horizontal\;distance})$$
Where,
Vertical distance = the distance of the line of sight between observer and the object,
Horizontal distance = the horizontal distance between the observer and the object.
So, we can calculate the angle of depression with the knowledge of vertical and horizontal distance between the observer and the object.
How to find the Angle of Depression?
The angle of depression can be calculated by using the inverse tangent of ratio between vertical and horizontal distance between the observer and the object that is written as
$$ θ\;=\;tan^{-1}\;(\frac{vertical\;distance}{horizontal\;distance})$$
See the following examples to understand the concept of angle of depression.
Example#1
A man was standing on the top of a building at a height of 70m from the ground. When he jumped from the top of the building, he fell at a horizontal distance of 70m from the building. Find the angle of depression.
Here,
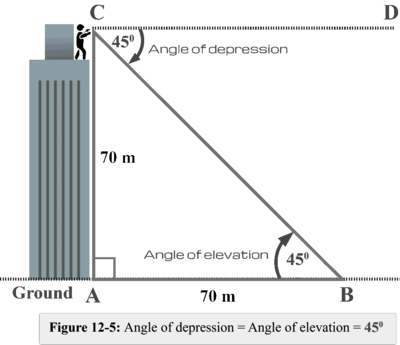
vertical distance = h = 70m
horizontal distance = d = 70m
By using the formula of angles of depression as
$$ θ\;=\;tan^{-1}\;(\frac{h}{d})$$
Substituting the values of h and d.
$$ θ\;=\;tan^{-1}\;(\frac{70}{70})\;=\;tan^{-1}\;(1)$$
$$ θ\;=\;45^o $$
Example#2
A man at the top of a building having height 50ft from the ground, looking at another man who is 39ft from the building. Find the angle formed by these two men.
Given that,
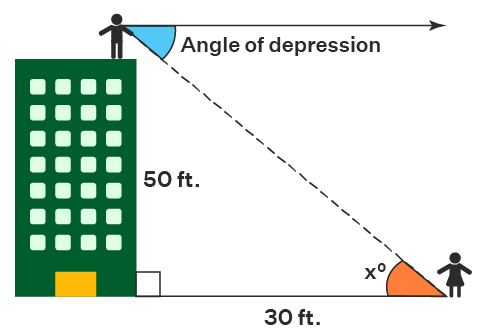
height (h) = 50ft
distance (d) = 30ft
Angle of depression can be calculated as
$$ θ\;=\;tan^{-1}\;(\frac{h}{d})$$
$$ θ\;=\;tan^{-1}\;(\frac{50}{30})$$
$$ θ\;=\;59^o $$
FAQ’s
Is the angle of depression and elevation the same?
No, the angle of depression and elevation is not the same. It is because the angle of depression is the measure of angle between vertical and horizontal distance where the object is at the lower level to the observer. But the angle of elevation is the angle between the object and observer where the object is at upper level.
What is the angle of depression in trigonometry?
The angle of depression is the measure of angles between a horizontal line and the vertical line in downward direction.
What is the maximum angle of depression?
The angle of depression must be equal or less to 90 degrees. It means that the maximum angle of depression is 90.
What is the formula for angle of depression?
The formula to calculate angle of depression is that
θ = tan-1 (vertical distance / horizontal distance)
Is the angle of depression negative?
No, the angle of depression cannot be negative. It is only in the lower direction to the observer.
Is the angle of depression and elevation equal?
Yes, the angle of depression and elevation can be equal because they are congruent to each other if both are related to the same location.