Are Vertical Angles Congruent: Examples, Theorem, Steps, Proof

Are Vertical Angles Congruent?

As we know that vertical angles are opposite and equal to each other. Here we will prove that vertical angles are congruent to each other.

What are Congruent Angles?

Two angles are said to be congruent if they have equal measure and oppose each other.

Vertical Angle Congruence Theorem

Vertical angles congruence theorem states that when two lines intersect each other, vertical angles are formed that are always congruent to each other.

Find this detailed blog for learning more about the vertical angle theorem.

Vertical Angle Congruence Theorem Example

Are vertical angles congruent? Let’s prove it.

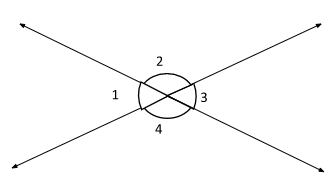
Consider the two lines AB and CD intersecting each other at the point O. The vertical angles are formed. We have to prove that:

$$ m∠1 \;≅\; m∠3 $$

And

$$ m∠2 \;≅\; m∠4 $$

Since the measure of angles 1 and 2 form a linear pair of angles. So,

$$ m∠1 \;+\; m∠2 \;=\; 180 $$

Similarly, the measure of angle 2 and 3 also form a linear pair of angles,

$$ m∠2 \;+\; m∠3 \;=\; 180 $$

Now by using the transitive property, we can say that:

$$ m∠1 \;+\; m∠2 \;=\; m∠2 \;+\; m∠3 $$

Simplifying,

$$ m∠1 \;=\; m∠3 $$

Hence we can write,

$$ m∠1 \;≅\; m∠3 $$

The reason is that the equal and opposite angles are called congruent angles. It is denoted by ‘≅’.

FAQ’s

How do you know if the angles are congruent?

If two angles have equal measure and opposite to each other then they will be congruent angles.

Can you calculate vertical angle on a calculator?

Yes, you can calculate vertical angle on a calculator easily. You need to enter the angle values, and the calculator will instantly show you accurate results.

Does the congruent mean equal?

The congruent means equal and opposite to each other. It refers to the same shape. But it does not mean equal because the direction of angles is opposite.

Are vertical angles congruent or complementary?

The angles formed by the intersection of two lines are always congruent to each other because they are equal in measure and oppose to each other.

Are Vertical Angles Congruent: Examples, Theorem, Steps, Proof

Table of contents