What are Vertical Angles?
When two lines intersect each other on a point in such a way that four angles are formed. Those angles oppose each other and are equal in measurement. These four angles, if they are equal and opposite to each other without sharing any side, are called vertical angles.
Vertical Angles Definition
Vertical angles are formed when two lines intersect with a common vertex and are opposite to each other. These lines make the same angles with each other when they intersect.
In other words, they are always congruent, which means they share some angle measure.
For example, in the following figure, the measure of angle 1 and 2 are vertical angles because they share the same vertex point and also have some measure of the angle.
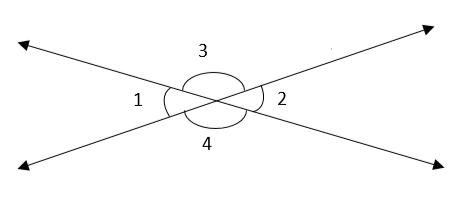
Similarly, the measure of angle 3 and 4 are also vertical angles and are congruent having the same vertex. We can also write it in mathematical form as:
$$ m∠1 \;=\; m∠2 $$ $$ m∠3 \;=\; m∠4 $$
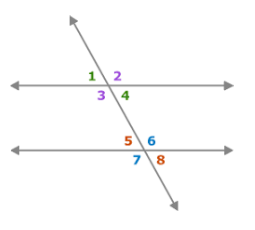
See another example below:
In the following figure, there are two parallel lines intersected by another line. The measure of angle 1 and 4 are congruent to each other and also the measure of angle 2 and 4.
These are vertical angles. Similarly for the bottom pairs of angles 5 and 8 are same and oppose each other also the measure of 6 and 7.
Some key points about Vertical Angles
- Vertical angles are formed by the intersection of two lines.
- The lines share a common point but do not share any side.
- Vertical angles are always congruent.
- Parallel lines never intersect.
- You can find the missing angles with the help of vertical angles.
- The two neighbouring angles are supplementary because their sum is always 180.
How to Find a Missing Angle?
You can find the missing angle between two lines intersecting each by using the properties of vertical angles. Consider the following example to understand how the missing angle can be found.
Example#1
In the following figure, calculate the unknown angle x.
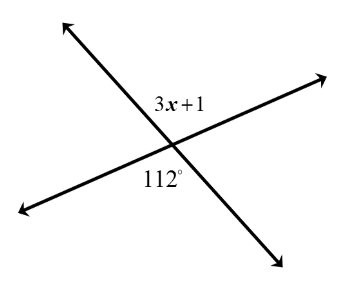
The given figure shows that two lines intersect each other. So they formed vertical angles.
Using the property of vertical angles, the angles are congruent so,
$$ 3x \;+\; 1\; =\;112 $$
Where x is the unknown perimeter. Now calculating the value x,
$$ x \;=\; \frac{111}{3} \;=\; 37 $$
Now by using the value of x, we can verify that these angles are congruent or not. So,
$$ 3x' \;+\; 1 \;=\; 3(37) \;+\; 1 $$ $$ 3x \;+\; 1 \;=\; 111 \;+\; 1 \;=\; 112 $$
Hence we can write,
$$ m∠(3x \;+\; 1)^o \;=\; m∠112^o $$
Related: Vertical Angle Theorem - Definition, Examples, Proof with Steps
Example#2
Calculate the value of x such that two lines intersect at the common point R.
In the given figure, the line PT and SQ intersect each other at the vertex R. So, using the properties of vertical angles,
$$ m∠PRS \;=\; m∠QRT $$
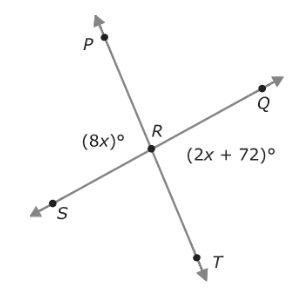
Similarly,
$$ m∠PRQ \;=\; m∠SRT $$
So, we can write that:
$$ m∠(8x)^o \;=\; m∠(2x \;+\; 72)^o $$ $$ 8x \;=\; 2x \;+\; 72 $$
Calculating the value of x.
$$ 8x \;-\; 2x \;=\; 72 $$ $$ 6x \;=\; 72 $$ $$ x \;=\; 12 $$
By using the value x,
$$ m∠PRS \;=\; 8x \;=\; 8(12) \;=\; 96 $$ $$ m∠QRT \;=\; 2x \;+\; 72 \;=\; 2(12) \;+\; 72 $$ $$ m∠QRT \;=\; 24 \;+\; 72 \;=\; 96 $$
Hence,
$$ m∠PRS \;=\; m∠QRT $$
The given lines form vertical angles that are congruent to each other. You can also use an online tool to calculate vertical angles. There are a lot of related and useful online tools available on this website which you can use for free.
FAQ’s
What is vertical angle in maths?
The vertical angles are the corresponding angles sharing a common point and have an equal measure of angles.
Are vertical angles congruent?
Yes, the vertical angles congruent. When two lines intersect each other, they share the same and equal angles between them.
How many vertical angles are there when two lines intersect?
There are four vertical angles formed by the intersection of two lines. The sum of two neighbouring angles is 180°. So, the total degrees of four vertical angles are 360°.
Are the vertical angles supplementary?
Yes, the vertical angles are supplementary. It is because the sum of two neighbouring angles is 180. Two angles are called supplementary if they add up to 180.