Introduction
The vertical angles follow the congruent theorem which states that when two lines intersect each other, their share same vertex and angles regardless of the point where they intersect. In this article, you will be able to prove the vertical angle theorem.
What is Vertical Angle Theorem?
“In a pair of intersecting lines, the vertically opposite angles are congruent.”
It states that the opposing angles of two intersecting lines must be congruent or identical. It means that regardless of the intersecting point, their opposite angles must be congruent. They will have same amount of angles but with opposite direction.
Explanation of the Theorem of Vertical Angles
According to the vertical angles theorem, when two lines intersect each other they make equal and opposite equal to each other and the sum of two neighbouring angles is 180°. The equal and opposite angles are called congruent angles.
Let’s prove it.
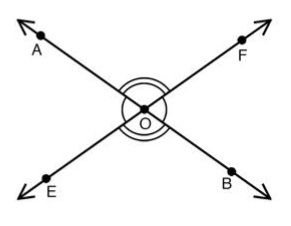
Consider two lines AB and EF intersecting each other at the vertex O.
We have to prove that:
$$ m∠AOE \;=\; m∠BOF $$
And
$$ m∠AOF \;=\; m∠BOE $$
Proof
Given that AB and EF are intersecting the centre common point O. Since m∠AOE and m∠AOF for a linear pair, so they are supplementary angles. Using the supplementary angles:
$$ ∴m∠AOF \;+\; m∠BOF \;=\; 180^o \; \; .......... (1) $$
Similarly for m∠BOF and m∠BOE, we can write,
$$ ∴m∠AOF \;+\; m∠AOE \;=\; 180^o \; \; .......... (2) $$
Now using the 1 and 2, we get:
$$ m∠AOF \;+\; m∠BOF \;=\; m∠AOF \;+\; m∠AOE $$
By simplification, we get:
$$ m∠BOF \;=\; m∠AOE \;\; .......... (3) $$
Now similarly,
$$ m∠BOF \;+\; m∠BOE \;=\; 180^o \; \; .......... (4) $$
And, from 1 and 4. we get:
$$ m∠AOF \;+\; m∠BOF \;=\; m∠BOF \;+\; m∠BOE $$
Simplifying,
$$ m∠AOF \;=\; m∠BOE \; \;...........(5) $$
Hence, from the equation 3 and 5 we can conclude that vertical angles are always congruent to each other.
Related: Also learn more about vertical angles with different examples.
Example
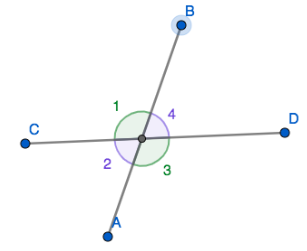
In the given figure, two lines AB and CD are intersecting each other and make angles 1, 2, 3 and 4. These pairs of angles are congruent i.e. equal and opposite to its corresponding angle such that:
$$ m∠1 \;=\; m∠3 $$
And
$$ m∠2 \;=\; m∠4 $$
So, these are vertical angles.
Properties of Vertical Angles
Vertical angles are formed when two lines intersect each other. They have two important properties. These are following properties.
- Their sides can be determined by same lines.
- They share same vertex but not a same side.
Uses of Vertical Angles
They have many uses in our daily life. For example,
- In the alphabet X.
- In a kite to hold it properly with two sticks.
- In rail road crossing signs.
- In open scissors pliers.
- In measuring missing angles between two lines that are formed by their intersection.
Why are Vertical Angles Always Congruent?
The congruent theorem says that the angles formed by the intersection of two lines are congruent. It is because the intersection of two lines divides them into four sides. Every side has an angle and two adjacent sides will have same angles but they will oppose each other. It is the basic definition of congruency. Therefore, the vertical angles are always congruent.
FAQ’s
Do vertical angles add up to 180 degrees?
Yes, the vertical angles add up to 180 degrees. It is because two neighbouring angles are supplementary and their sum will be 180.
What is the linear pair theorem?
The linear pair theorem states that if two angles form a linear pair, they are supplementary and add up to 180°. So in vertical angles, the measure of two angles add up to 180 therefore they satisfy the linear pair theorem.
Why are vertical angles always equal?
The vertical angles are always equal because they are formed when two lines intersect each other at a common point. They are always equal and opposite to each other, so they are called congruent angles.
What is postulate and theorem?
A postulate is a statement that can be proved true or false without any explanation and proof. Whereas, a theorem is another kind of statement that must be proven.
We hope you liked this article and it helped you in learning more about vertical angles and its theorem. This website offers you an online tool to calculate vertical angle and its theorem.