What is Dilation in Math?
Introduction
Dilation is a process of transforming geometrical shapes that depends on the scale factor. It is done by shrinking or stretching the shapes. This article will help you to understand the dilation, centre of dilation and the scale factor.
Dilation Definition
A dilation is a stretch or a shrink of an image. The stretch means making the image larger, and shrink means making it smaller.
In mathematics, dilation transforms a geometrical shape that makes it small or big according to the scale factor. The shape remains the same in this transformation, but the size will be decreased or increased by a specific ratio.
Unlike other transformations, dilation is not a change in orientation and is not a change is not in shape. It has applications in photography, art, craft etc.
Centre of Dilation
The dilation in geometry transforms a shape by stretching or shrinking its size. When we dilate an image, we must fix a point to which we can change the size. That fixed point is called the centre of dilation. It is an important part that has a visible effect on the dilation scale factor.
Dilation Scale Factor
While dilating an image, a specific amount or ratio is used that is proportional to the original image's size, called the dilation scale factor. It is also defined as the ratio of the new image's size to the original image's size. The larger the scale factor, the larger the image's size. Similarly, a smaller scale factor makes the size smaller. The scale factor is represented by k.
- When k is unchanged, the size of the image will be unchanged.
- When k is greater than 1, the image size will stretch outside.
- When k is less than 1, the image will shrink from the inside.
Scale Factor Formula
Suppose an image has been dilated. It is important to determine the scale factor that produced the image. For example, in animation, if an object moves toward the screen, every part of the object should dilate accordingly.
To find the scale factor of an image or shape, the following formula is used.
(pre - image side length) × (scale factor) = image side length
Or,
$$k\;=\;\text{scale factor}\;=\;\frac{\text{image side length}}{\text{pre - image side length}}$$
Properties of Dilation
Dilation in mathematics changes the size of an image without changing its orientation or shape. There are some important properties of dilation that are:
- It does not change the angle of an image.
- The midpoint of the original shape will remain the same after dilation.
- After dilation, the image size will either be reduced or increased only. It does not change the shape.
- It does not rotate the image after dilating it.
How to do Dilation in Geometry?
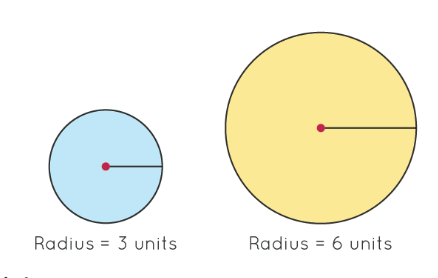
The dilation of a shape depends on the determination of scale factor. The variation of image size increases or decreases with the scale factor that is determined by finding the ratio of new image size and original size. That is:
$$k\;=\;\frac{\text{image side length}}{\text{pre - image side length}}$$
For example, in a circle the scale factor is its radius. It is because the size of the circle depends on the radius. If the radius of the circle is 3cm and the scale factor is 2 then how much the circle will be dilated.
By using the scale factor formula we know that,
(pre-image side length) × (scale factor) = image side length
Here,
3 × 2 = 6
So the new circle size will be of radius 6cm.
FAQ’s
What is the Rule for Dilations?
The transformation of geometrical shapes depends on the dilation scale factor. The scale factor follows three rules to transform any shape. These rules are:
- When k is unchanged, the size of the image will unchanged.
- When k is greater than 1, the image size will stretch outside.
- When k is less than 1, the image will shrink from inside.
Can Dilations have a Negative Scale Factor?
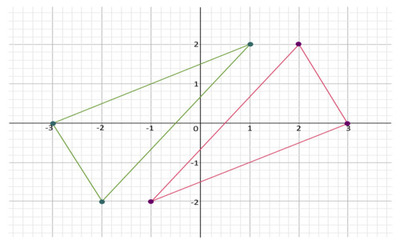
Yes, the scale factor can be negative. Dilation of a shape with negative scale factor produces an image in the opposite direction of the original image. For example a triangle with a negative scale factor will produce an image that is shown in figure.
What is Dilation in Geometry?
In geometry, the dilation is a process of transformation of an image without changing its orientation. It increases or decreases the size of an image without rotating it or changing its angle.