How to do Dilation in Geometry? - Transform an object's size

How to do Dilations in Geometry?

Introduction

Dilation is the process of increasing or decreasing the size of an object. An object can be dilated by using the dilation scale factor. In this article, you will learn how to transform an object and identify the type of dilation.

Before understanding the dilation process, it is important to learn how to identify the type of dilation and calculate the scale factor.

Determination of Dilation Type

The type of dilation affects the shape and orientation of an image. The scale factor determines the dilation type. There are two types of dilations. That is:

1. Expansion
2. Contraction

Expansion

The expansion of dilation is a process of transforming an image that increases its size. The scale factor identifies it. If it is greater than 1, the dilation will expand the image size.

Contraction

The contraction of dilation is the transformation of an image that decreases its size. If the scale factor k is less than 1, the dilation will reduce the image size.

How to find the Scale Factor?

The scale factor of a dilation is an amount of increment or decrement of the image size. It can be calculated by dividing the new image size by the original size, and it is denoted by k, expressed as;

$$k\;=\;\frac{\text{New image size}}{\text{Pre - image size}}$$

For example, the image size is 2 units and the new size is 6 units. The scale factor will be 3 units.

Steps of Dilation

Dilation of a geometrical shape depends on the scale factor that enlarges or reduces it. It is done by using the following steps.

1. Find the scale factor using the formula;
2. $$k\;=\;\frac{\text{New image size}}{\text{Pre-image size}}$$
   • New image size is the size of the image after Dilation.
   • Pre-image size is the size of the image before Dilation.
3. Identify the type of Dilation by using the dilation rules.
4. Multiplying the scale factor with the original image size to get dilated image size.

Here are some examples that will explain how to do Dilation.

Dilation in Coordinate Plane

Suppose we have to transform geometrical shapes in the coordinate plane. Let’s discuss how to dilate in the coordinate plane.

Example # 1

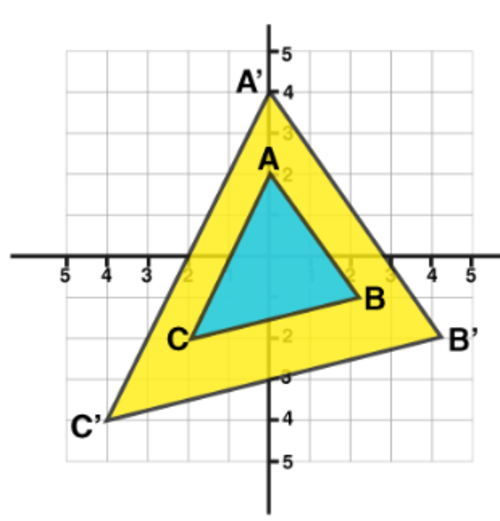
Let ABC be a triangle in the coordinate plane and the origin (0, 0) be the centre of dilation. Suppose we choose scale factor 2 for dilation. The coordinates of the triangle are A(0, 2), B(2,-1) and C(-2,-2). To transform this triangle, we will use the scale factor formula. That is:

$$k\;=\;\frac{\text{New image size}}{\text{Pre-image size}}$$

Since the scale factor is known then,

(pre - image size) × k = new image size

It means that we can get new coordinate points of the triangle by multiplying the scale factor with original coordinate points. Hence new coordinate points are A'(0, 4), B'(4,-2) and C'(-4,-4). Since the scale factor 2 is greater than 1 that means the shape of the triangle will expand by 2.

Example # 2

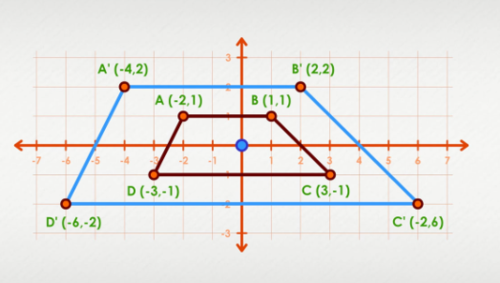
Suppose ABCD be a trapezoid with centre of dilation at origin (0, 0). Also suppose that the scale factor is 2. The pre-image coordinates of trapezoid are A, B, C and D having points (-2, 1), (1, 1), (3, -1) and (-3,-1) respectively.

Now by using the scale factor formula we obtained new coordinates of trapezoid that are A'(-4, 2), B'(2, 2), C'(6, -2) and D'(-6,-2). The size of the trapezoid will be doubled then the original. The graphical representation of the new image size is shown in figure.

Dilation not in Coordinate Plane

When there is not a coordinate plane, let’s see how to do dilation in geometry without coordinate plane.

Example # 3

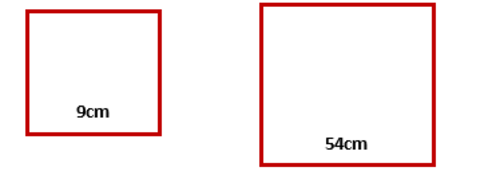
Suppose a preimage of a polygon with a side AB of 9cm long and the scale factor is 6. Here we are taking only one side of a polygon because all sides of the polygon are the same. We need to check how it will be transformed with the scale factor 6.

By scale factor formula,

(pre - image size) × k = new image size

We get,

(9 cm) 6 = 54cm

So the new image of the polygon will be 54cm longer than the pre-image.

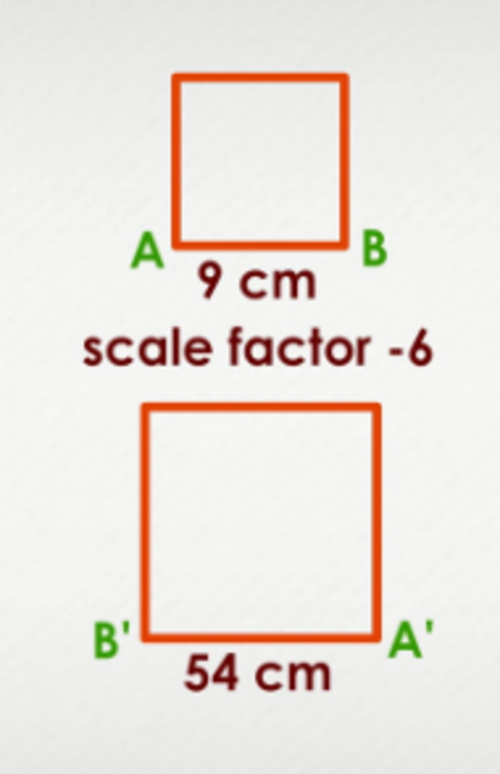
Suppose if we have a negative scale factor in this example, then the new side will be opposite the centre of dilation from the pre-image. Then we will obtain the following image.

FAQ’s

What are the Two Types of Dilation?

There are two types of dilation. The image will be expanded if the scale factor is greater than 1. This type of dilation is called Expansion. If the scale factor is less than one, the image will be reduced, and this type of dilation is called contraction.

What kind of Transformation is a Dilation?

Dilation is a transformation that changes the size of an image without changing the shape and orientation of the image. It can expand or contract any image. The dilation of a geometrical shape depends on the dilation scale factor.

Is Dilation a Rigid Transformation?

No, dilation is not a rigid transformation. The rigid transformation moves an image with a scale factor but does not change the shape or the orientation of the image. The dilation only changes the size of the image without changing its shape or orientation.